Snake (source)

Why?

When I taught Junior High, when the students finished their work they could play games on the computer. Cool Math was something that the school allowed and a lot played snake. During state testing the kids take a 3 hour test (or at least have to sit in a room for 3-4 hours). To make test days more fun, I had my afternoon classes play the snake game and record all of their scores and times. The "educational" purpose of this activity was to 1) use a spreadsheet (Google Sheets) and 2) gather data. They used their data (over several days) to plot their Score vs. Time and to make a histogram of their scores. I wanted them to see the correlation between their score and time played (mostly a straight line) by looking at plotted points. I also wanted them to see that their scores fell into a normal distribution (around some "average" that they usually were able to achieve). The second part, about the normal distribution, I did not expect the students to understand. It was more of a "I'm going to predict all of your data will look similar to this" and then it did.

So I initially had the students open a Google Stopwatch, start it, play the game, then they had to stop it (when they died) and record the time and the score. I joked with the students that, "I guess I should just make my own with a timer." They basically dared me to try and replicate the snake game—so I did—and I did it better!

Cool Math Snake Game—Realizations

It was pretty obvious by the square tiles that the snake game was on an integer grid made up of spaces that were 1) occupied, 2) empty, or 3) an apple (or red target). For graphics, I needed three basic things: 1) how big are the squares, 2) how much width between squares, and 3) how big is the board? I got those from screenshots and the colors from the Google Chrome extension: ColorPick Eyedropper

A Discrete Grid is a More Significant Epiphany Than it Appears

It's significant because trying to represent a snake in a continuous domain presents many challenges while representing in a discrete space is easy!

Detecting a Collision is Difficult

If the domain is real numbers, then the snake is an infinitesimal line (or you can make it even more complicated); even with the restriction of "Etch A Sketch" (only right angle turns), the best you can do is represent the line by a finite set of points (that make the entire snake). Even assuming infinite precision at all times (unrealistic), i.e. we can detect whether or not the snake has occupied the same square as another, the point will have to be tested against every equation of a line between each point in the snake representation. So this operation, regardless of how long the test itself takes, takes a linear time relationship with the points for the snake and, thus, grows, in time, with the length (or complexity) of the snake structure.

Realistically, we have to test a "new" segment against all others:

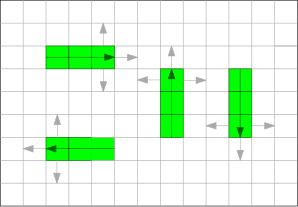
The solid black segments represent the snake already in existence and the gray lines with arrows represent a possible traversal. We can visually see, where there are three down arrows, that between those two points (going across the bisected segment), we have hit the snake and should end the game. Every segment has to be tested to determine a collision here (this isn't as easy at is seems).

There is a further complication: input events. There is time between the two points to press down (or up) to avoid the collision (the two different grayed dashed lines going down). Even if this input event happens in time (the right-most down arrow in the picture), it won't register until it's too late and will still cause a collision. Ultimately, this type of error is inevitable but it can be minimized!

A Discrete Grid Greatly Simplifies Things

Looking at the (extremely) simplified example below, the worst case scenario for checking collisions is always the number of tiles on the board. This suggests several things. The first is we can immediately do better than testing every tile: we can simply test every snake tile (the length of the snake). This first realization, suggests yet two more things: a) the snake should be a list of tiles and b) the tile itself can hold the information about whether or not it's part of the snake.

This lead me to use a Doubly LinkedList to represent the snake as a Deque of "tiles". A Deque was the most appropriate data structure because it's naturally a FIFO queue.

First Optimization: Strongly Couple Snake and Board

At first, it seems like a good idea that the board remain abstract or that the snake simply hold each "tile" object. It's simple to advance the snake: 1) take off the last tile (freeing it up) and then 2) add a tile to the head. Then I check for collisions with the set of tiles in the snake itself. But there's a better way—what if we just knew whether or not the tile was occupied (without a search)?

Combine Snake and Board, Let Them Interact

Rather than have an abstract board, create concrete SnakeSquare objects; these objects represent every possible square on the board. These objects hold three pieces of information: 1) occupied or not, 2) apple or not (it cannot both be occupied and an apple), and 3) coordinates (so that I can easily use the board to access neighbors). In this way a "snake" can be defined by a sequence of SnakeSquare objects.

You can then pretend like the snake leaves "footprints" on the board. So the board is completely unaware of the snake structure, while the snake sets the occupied parameter of each SnakeSquare, thus the board is constantly being modified by the snake object. Meanwhile, the board itself can tell you (immediately) whether or not a particular tile is occupied, holds an apple, or not.

First Challenge: Responsive Controls

Making the snake move is fairly simple and steering it starts out simple enough. Below, you see there are four possible directions for the snake to be moving in and each direction allows a different set of moves (each one excludes turning back on itself—a problem I had to see happen to realize it was a problem).

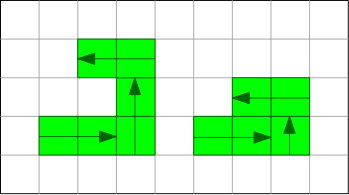
So there are four headings: right, up, left, down. The heading determines which of the three tiles the head of the snake will occupy next. You can steer the snake by pressing the arrow keys and change the heading (unless you try to turn it back on itself, which is ignored). Consider the two maneuvers in the picture below: Left) you must time it (wait to press to the left so that you skip a tile) and Right) you must press left as soon as you enter the above (up) square—does this need to be timed?

Second Optimization: Cache Key Strokes

In my first attempt, I changed the heading when the key was pressed. The effect this had was that it was possible for me to press the keys so fast, that I could cancel out a key press by pressing more than once while the snake was waiting to advance. I noticed that when I tried maneuvers like the above right, it usually worked, but often did not.

To solve the problem, cache key strokes. Use a FIFO list to hold key strokes. Below shows the code when a key is pressed. headingQueue is a Deque (LinkedList).

public void setHeading(final int heading) { 
	if (alive) 
		headingQueue.add(heading);
}
				

To use this, when I advance, I set the heading of the snake from this cache (if it's empty, don't change the heading). The code snippet below shows that the headingQueue is emptied until it finds a valid heading. If found, it changes the snake's heading. If no valid heading is found, headingQueue will be empty after this and the snake's heading will remain unchanged (or headingQueue was already empty and, again, there's no change).

int newHeading;
while (!headingQueue.isEmpty()) {
	if (isValidHeading(newHeading = headingQueue.pollFirst())) {
		heading = newHeading;
		break;
	}
}
				

Second Challenge: Graphics for a Cloud VM

I've done video graphics numerous times before and I generally use the approach like a video camera: I separate the simulation and then the graphics part is displayed by taking snapshots of the simulation. I did this here and it worked fine on my computer but it was really bad on the VMs. Basically the game looks fine so long as the sample rate of the video (frames per second) is faster than the rate at which the snake moves one square. The problem for the VMs is that the network can't handle such a high refresh rate.

Final Optimization: Strongly Couple Game and Graphics

I hated doing this. I did not like the idea of combining both my snake game (simulation) with the graphics part. But for optimal performance I didn't see any other (reasonable) way. For the most part, the graphics only change when the snake advances. This creates a new green square in the direction of its heading and deletes the last square from the snake (and marks it as unoccupied). There are a few other cases that need to be handled but I'm not going to go into those: what happens when you hit an apple; yourself; the border; etc.

So now there is a single thread, which only updates the graphics when the snake advances. Furthermore, I only update the part of the graphics that needs to be updated. You see Graphics g —that is to an internal raster (a BufferedImage). The panel paints itself by simply drawing that raster. So you see two calls to fillRect . The first fills a rectangle with the padding color and the second fills a (slightly) smaller rectangle with the snake color. This gives the effect of a padding around the snake. Finally, I repaint that square that just got changed.

To move the end of the snake, I just have to delete that square. One simple call to fill a rectangle with the background color and then repaint just that section. This also shows how it's easy to grow the snake. Every advancement, the snake moves forward. If an apple is eaten, then I simply do not delete the end of the snake for a number of rounds.

private void drawSnake(final SnakeSquare square) {
	final int x0 = (square.i + 1) * snakeSquare;
	final int y0 = (square.j + 1) * snakeSquare;
	g.setColor(PADDING_COLOR);
	g.fillRect(x0, y0, snakeSquare, snakeSquare);
	g.setColor(SNAKE_COLOR);
	g.fillRect(x0 + padding, y0 + padding, snakeSquare - 2 * padding, snakeSquare - 2 * padding);
	repaint(x0, y0, snakeSquare, snakeSquare);
}

private void deleteSnake(final SnakeSquare square) {
	final int x0 = (square.i + 1) * snakeSquare;
	final int y0 = (square.j + 1) * snakeSquare;

	g.setColor(BG_COLOR);
	g.fillRect(x0, y0, snakeSquare, snakeSquare);
	repaint(x0, y0, snakeSquare, snakeSquare);
}
				

snakeSquare is an int graphics field which holds the size of the squares in pixels (padding including).